- Observación del Problema
- Formulación de la Hipótesis
- Comprobación de la Hipótesis
- Demostración o refutación (antítesis) de la hipótesis.
- Tesis o teoría científica (conclusiones).
La estadística influye directa e indirectamente en todos o casi todos los pasos del método científico
de manera directa influye en la formulación de la hipótesis y la formulación del problema.
Tema 2
Reseña Histórica
La estadística Comienza hace mucho tiempo en la prehistoria con la necesidad del hombre de conocer sus recursos, en la prehistoria era muy sencilla ya que solo contaban a las personas dela tribu, sus animales y objetos, los Nuragas, al rededor del 3.500 A.c llevan cuentas de su ganado y de la caza, luego los Egipcios, evolucionados un poco mas empezaron a recolectar datos de la población y datos de las riquezas, ademas según algunos historiadores Ramses II, ordeno realizar un censo de la tierra para realizar nuevos repartos de las mismas, Luego los Babilonicos, cerca del 3000 a.c, empezaron a recolectar datos de las producciones agrícolas, y sus ventas o trueques agrícolas, los Chinos en el 2000 a.c empezaron a censar a su población, Los Griegos, al rededor del 600 a.c, ordenaron censos periodicos ya que vieron que organizar censos muy continuos era muy costoso, ellos lo hacían con fines tributarios, los derechos del Voto, y ponderar su poder militar, aunque los Romanos, Fueron los padres de la investigación Estadística. en adelante siguió evolucionando de acuerdo a las necesidades de cada gobernante, y se empleo en políticas publicas y esto nos dio a la estadística como la conocemos hoy
La Bioestadistica
El primero en utilizar la estadística con fines de salud fue Pierre Charles-Alexander Louis, quien la aplico para un caso de tuberculosis, luego de este estudio surgieron muchos mas en la aplicacion de la estaditistica en la rama de la salud y nacieron nuevas ramas como la epidemiologia, la demografía, entre otras.
La Estadística: Se divide en 2 grandes grupos que son;
-Estadística Descriptiva: Describe los datos de la muestra, y estos datos pueden ser resumidas numérica o gráficamente, es decir procedimientos mediante el cual se puede organizar y resumir conjuntos de observaciones en forma cuantitativa.
--Estadística inferencial: Es utilizada para resumir o sacar cuentas basándose en los datos obtenidos a partir de una muestra
(pequeña parte de la población), son cálculos aritméticos realizados acerca de los valores obtenidos en proporción con toda la población
Método Estadístico:
Es el metodo utilizado para la realizacion de estudios estadistico con el fin de llevarlo de la mejor y mas organizada manera, ademas de tratar de reducir los costos de los estudios al minimo su pasos son:
- Problema
- Planificación
- Objetivos
- Hipótesis de la investigación
- Determinar la población y muestra
- Recolección y codificación de Datos
- Análisis e interpretación de datos
- Presentación de los resultados
- Elaboración del reporte de investigación
Términos Del Estudio Estadistico
Poblacion (N): Es a quien vamos a estudiar, la población la cual es el objetivo de nuestro estudio estadistico, debe poseer una o varias propiedades similares, se clasifica en 2, una
Población Finita, es aquella poblacion que pose un numero determinado y la
Población infinita, es aquella población que no se conoce la cantidad de individuos
Muestra (n): Es un grupo de elementos o de individuos de una población que se toma para hacer el estudio de la población general.
Datos (Xi): Son cada uno de los elementos o datos que integran una muestra determinada
Unidad Estadística: Son cada uno de los elementos o datos que integran una población determinada
Tema 3
Escalas de Medición y Variables Estadísticas
Escalas: Es una sucesión de niveles de intensidad de un objeto de la misma especie, ejemplo la escala del ph, varia su intensidad pero sigue siendo el mismo objeto de estudio
Medición: Es agregarle números o cuantificar un objeto de a cuerdo a reglas preestableciodas, ejemplo, el metro
Escalas de Medición:
- Nominal
- Ordinal
- Intervalo
- Razon
Escala Nominal: Son dicótomicas por lo tanto no ordenables (si o no, Sano o enfermo)
Escala Ordenal: Porque sus categorías están ordenadas sucesivamente (1,2,3,4)
Escala de Intervalo: Son parámetros de escalas, es decir, que el cero no representa ausencia de la característica (Cero Arbitrario), ejemplo, escalas de temperatura
Escala de Razón: Es Cuantitativa, es decir el Cero Representa ausencia de la propiedad (Cero Absoluto)
Variable
Es Algo que no es constante, es una propiedad que puede fluctuar y cuya variación es susceptible de medirse
Variables Estadísticas
Variables Cualitativas: Clasifican los elementos de la muestras en Categorías y se dividen en
Ordinales, Aquellas cuyas características pueden ser organizadas y
Nominales, Aquellas cuyas categorías no pueden ser ordenadas
(Dicotomicas)
Variables Cuantitativas: Clasifican los elementos de la muestra de manera numerica o cuantificable y se deividen tambien en 2,
Discretas, aquellas en las que no existes valores intermedios entre 2 valores consecutivos,
Continuas, Existen Valores intermedios entro 2 valores seguidos
Experimento
Es una situacion de control sobre las cuales se cambian de manera intencional una o mas Variables Independientes (Causas), para analizar las consecuencias en las Variables Dependientes (Efectos)
Variables en un Experimento
Variable Independiente: Son las Causas del efecto que se esta investigando, es el centro de la investigación y no depende de otra variable
Variable Dependiente: Esta subordinada a otra variable que si cambia la otra esta varia
Variables Intervinientes: Son aquellas que pueden tomar parte en el estudio o investigación
Tema 4
Planificación y Ejecución de Investigaciones Medidas
Planificación: Es un elemento necesario para el desarrollo de las cosas, es decir la organización necesario para llevar a cabo determinada acción
La planificación para la ejecución de estudios Bioestadisticos o Estadísticos en general es sumamente importante ya que sin ella se harían las cosas desorganizadamente lo que haría que cometiéramos muchos errores y nos llevaría a perder tiempo y dinero en exceso en estos estudias, para ello se ha desarrollado una serie de pasos tomando en cuenta cosas como, la recolección de datos, elaboración, análisis de la información, tiempo, presupuesto, todo esto con el fin de evitar improvisaciones durante el desarrollo de la investigación
Pasos para la Planificación
- Planteamiento del problema
Primero que nada debemos determinar cual es el problema o la problemática que deseamos resolver o estudiar, y determinar su importancia, determinar el objetivo final y los objetivos inmediatos de la investigación hacerse preguntas como ¿Que? ¿Por que? ¿Para Que?
2. Búsqueda y Evaluación de la Información Existente
Se debe buscar o investigar si este estudio no ha sido realizado con anterioridad, o si tenemos materiales de apoyo o de que manera otros investigadores enfocaron su estudio, para asi no hacer el mismo trabajo que ya otros han hecho
3. Como evaluar el trabajo se debe preguntar
¿Quien hizo el trabajo?, ¿Por que lo hizo?, ¿Cual fue el material utilizado?, ¿Donde hizo el estudio?, ¿Cuando se hizo?, ¿Como fue realizado?, ¿Cuantos individuos se estudiaron?, ¿Que conclusiones se obtuvieron?
4. Formulación de Hipótesis
Se debe desarrollar el supuesto a ser comprobado o la explicación provisional de los hechos que es lo que se intenta explicar
5. Verificación de la Hipótesis
Se debe verificar si esta hipótesis es cierta o no y si no lo es reformarla
6. Conclusiones, Recomendaciones y Referencias




![\operatorname{E}[X + c]= \operatorname{E}[X] + c \,\!](http://upload.wikimedia.org/math/8/5/a/85a00d2da36ee53533b8d5f1e9842642.png)
![\operatorname{E}[X + Y]= \operatorname{E}[X] + \operatorname{E}[Y] \,\!](http://upload.wikimedia.org/math/a/1/5/a15cbeacea501a46fb32656efc4a870c.png) (*)
(*)![\operatorname{E}[aX]= a \operatorname{E}[X] \,\!](http://upload.wikimedia.org/math/4/b/d/4bdd6ba758248cbe75c558a1a34fdec6.png)
![\operatorname{E}[a X + b Y] = a \operatorname{E}[X] + b \operatorname{E}[Y] \,\!](http://upload.wikimedia.org/math/2/3/d/23db5270f4369a806d5c98e254da0c3f.png)
 e
e 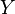 son variables aleatorias y
son variables aleatorias y  y
y 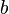 son dos constantes cualesquiera
son dos constantes cualesquiera



