Propiedades de la Esperanza Matematica:
Para poder definir las propiedades de la esperanza tenemos que saber bien que es la esperanza matemática, la definimos como el valor medio de una variable aleatoria, lo que quiere decir que es el valor que cruza la linea media de dos o mas valores completamente aleatorios, es decir cual es el la media de el valor que con mayor probabilidad vamos a obtener de una manera aleatoria,
Por Ejemplo:
Cual es el valor medio con que esperamos al lanzar 1 dado, de 6 caras.
sabiendo que tenemos igual probabilidades de obtener cualquiera de las caras, es decir 1/6
multiplicamos la probabilad por el valor de la cara del dado y se suman todos, el resultado sera la esperanza matematica.
Propiedades
1) Si el valor es 0, la esperanza siempre sera 0
Si X ≥ 0 y existe E(X), entonces E(X) ≥ 0
Esperanza de una función de una variable aleatoria
- Variable discreta

- Variable continua

- Linealidad de la esperanza matemática
- E(X + Y) = E(X) + E(Y)
- E(k · X) = k · E(X) para todo número real k.
- E(k) = k para todo número real k.
- E(a · X + b) = a · E(X) + b para todo par de números reales a y b.
- Esperanza del producto
- E(X · Y) = E(X) · E(Y) únicamente en el caso de que X e Y sean variables aleatorias independientes.
![\operatorname{E}[X + c]= \operatorname{E}[X] + c \,\!](http://upload.wikimedia.org/math/8/5/a/85a00d2da36ee53533b8d5f1e9842642.png)
![\operatorname{E}[X + Y]= \operatorname{E}[X] + \operatorname{E}[Y] \,\!](http://upload.wikimedia.org/math/a/1/5/a15cbeacea501a46fb32656efc4a870c.png) (*)
(*)![\operatorname{E}[aX]= a \operatorname{E}[X] \,\!](http://upload.wikimedia.org/math/4/b/d/4bdd6ba758248cbe75c558a1a34fdec6.png)
La esperanza es un operador lineal, ya que:
por ende:
![\operatorname{E}[a X + b Y] = a \operatorname{E}[X] + b \operatorname{E}[Y] \,\!](http://upload.wikimedia.org/math/2/3/d/23db5270f4369a806d5c98e254da0c3f.png)
donde  e
e 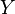 son variables aleatorias y
son variables aleatorias y  y
y 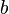 son dos constantes cualesquiera
son dos constantes cualesquiera
 e
e 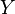 son variables aleatorias y
son variables aleatorias y  y
y 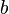 son dos constantes cualesquiera
son dos constantes cualesquiera
Ejemplo:

Propiedades de la varianza:
· σ2≥ La varianza es un valor positivo, como ya se ha comentado anteriormente, la igualdad sólo se da en el caso de que todas las muestras sean iguales.
· Si a todos los datos se les suma una constante, la varianza sigue siendo la misma.
· Si todos los datos se multiplican por una constante, la varianza queda multiplicada por el cuadrado de la constante.
· Si se disponen de varias distribuciones con la misma media y se calculan las distintas varianzas, se puede hallar la varianza total aplicando la fórmula
La varianza será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
Si a todos los valores de la variable se les suma un número la varianza no varía.
Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por el cuadrado de dicho número.
Si tenemos varias distribuciones con la misma media y conocemos sus respectivas varianzas se puede calcular la varianza total.
Propiedades de la Desviacion Estandar
Las Propiedades de la desviación estandar son muy similares a la de la varianza como veremos a continuacion
La desviación estándar será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.
- Si a todos los valores de la variable se les suma un número la desviación estándar no varía.
- Si todos los valores de la variable se multiplican por un número la desviación estándar queda multiplicada por dicho número.
- Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones estándar se puede calcular la desviación estándar total.


No hay comentarios:
Publicar un comentario