Distribucion de la Probabilidad

Uno de los principales objetivos de la estadística aplicada a la salud es la de reconocer y de estudiar las probabilidades, para asi de esta manera poder corregir y aplicar unas excelentes politcas de salud por eso debemos tener mucho cuidado al estudiar las distribuciones de las probabilidas, que no son mas si no que la regularidad con la que una poblacion presenta una variable que puede ser dependiente o independiente, es decir que al hablar de la distribucion de la probabilidad, es la herramienta con la que podemos determinar la probabilidad de un evento suceda o se repita en una poblacion estudiada, lo cual es de suma importancia para estudiar y aplicar estudios epidemilogicos en la poblacion

La distribucion de la probabilidad nos permite representar la informacion que actualmente se posee sobre un hecho especifico o un hecho real 

En la actualidad debido al alto indice de enfermedades se aplica estos estudios para obtener informacion y determinar probabilisticamente las enfermedades que se sucitan en una poblacion determinada

Ejemplo:

1.) De los pacientes que asisten al IAHULA 9 de Cada 10 presentan el virus de la chikunguya cual es la probabilidad de que tomando una muestra aleatoria de 12 pacientes solo 8 padescan de esta enfermedad

P(X=8) = 495. 0,0002

     = 0,0146

La probabilidad de que existan 8 con esta infección en una muestra aleatoria de 12 es de 0,0146. 

Asi sabremos determinar una mejor cifra epidemiologica, aunque ya sabemos que los valores de chikunguya son relativamente alto la probabilidas de que exactamente 8 pacientes en una muestra de 12 padescan esta infeccion es del 1 %  pero si lo estudiamos en una muestra de 10 personas cuantas la probabilidad de que el primer paciente que trates padesca de chikunguya es del 90%

Propiedades de La Varianza, Desviacion Estandar y Esperanza Matematica

Propiedades de la Esperanza Matematica:

Para poder definir las propiedades de la esperanza tenemos que saber bien que es la esperanza matemática, la definimos como el valor medio de una variable aleatoria, lo que quiere decir que es el valor que cruza la linea media de dos o mas valores completamente aleatorios, es decir cual es el la media de el valor que con mayor probabilidad vamos a obtener de una manera aleatoria, 

Por Ejemplo:

Cual es el valor medio con que esperamos al lanzar 1 dado, de 6 caras.

sabiendo que tenemos igual probabilidades de obtener cualquiera de las caras, es decir 1/6

multiplicamos la probabilad por el valor de la cara del dado y se suman todos, el resultado sera la esperanza matematica.

Propiedades

1) Si el valor es 0, la esperanza siempre sera 0

Si X ≥ 0 y existe E(X), entonces E(X) ≥ 0

Esperanza de una función de una variable aleatoria

1. • Variable discreta
   
   • Variable continua
   
2. Linealidad de la esperanza matemática
   • E(X + Y) = E(X) + E(Y)
   • E(k · X) = k · E(X) para todo número real k.
   • E(k) = k para todo número real k.
   • E(a · X + b) = a · E(X) + b para todo par de números reales a y b.
   
   
3. Esperanza del producto
• E(X · Y) = E(X) · E(Y) únicamente en el caso de que X e Y sean variables aleatorias independientes.


La esperanza es un operador lineal, ya que:

 (*)

por ende:

donde  e 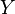 son variables aleatorias y  y 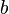 son dos constantes cualesquiera

Ejemplo:

Propiedades de la varianza:

·        σ2≥ La varianza es un valor positivo, como ya se ha comentado anteriormente, la igualdad sólo se da en el caso de que todas las muestras sean iguales.

·        Si a todos los datos se les suma una constante, la varianza sigue siendo la misma.

·        Si todos los datos se multiplican por una constante, la varianza queda multiplicada por el cuadrado de la constante.

·        Si se disponen de varias distribuciones con la misma media y se calculan las distintas varianzas, se puede hallar la varianza total aplicando la fórmula

La varianza será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.

Si a todos los valores de la variable se les suma un número la varianza no varía.

Si todos los valores de la variable se multiplican por un número la varianza queda multiplicada por el cuadrado de dicho número.

Si tenemos varias distribuciones con la misma media y conocemos sus respectivas varianzas se puede calcular la varianza total.

Propiedades de la Desviacion Estandar

Las Propiedades de la desviación estandar son muy similares a la de la varianza como veremos a continuacion

La desviación estándar será siempre un valor positivo o cero, en el caso de que las puntuaciones sean iguales.

• Si a todos los valores de la variable se les suma un número la desviación estándar no varía.

• Si todos los valores de la variable se multiplican por un número la desviación estándar queda multiplicada por dicho número.

• Si tenemos varias distribuciones con la misma media y conocemos sus respectivas desviaciones estándar se puede calcular la desviación estándar total.